Search

Sejarah

Label:


Akuntansi sebagai suatu seni yang mendasarkan pada logika matematik - sekarang dikenal sebagai “pembukuan berpasangan” (double-entry bookkeeping) - sudah dipahami di Italia sejak tahun 1495 pada saat Luca Pacioli (1445 - 1517), yang juga dikenal sebagai Friar (Romo) Luca dal Borgo, mempublikasikan bukunya tentang “pembukuan” di Venice. Buku berbahasa Inggris pertama diketahui dipublikasikan di London oleh John Gouge atau Gough pada tahun 1543.
Sebuah buku ringkas menampilkan instruksi akuntansi juga diterbitkan pada tahun 1588 oleh John Mellis dari Southwark, yang termuat perkataanya, "I am but the renuer and reviver of an ancient old copie printed here in London the 14 of August 1543: collected, published, made, and set forth by one Hugh Oldcastle, Scholemaster, who, as appeareth by his treatise, then taught Arithmetics, and this booke in Saint Ollaves parish in Marko Lane." John Mellis merujuk pada fakta bahwa prinsip akuntansi yang dia jelaskan (yang merupakan sistem sederhana dari masukan ganda/double entry) adalah "after the forme of Venice".
Pada awal abad ke 18, jasa dari akuntan yang berpusat di London telah digunakan selama suatu penyelidikan seorang direkturSouth Sea Company, yang tengah memperdagangkan bursa perusahaan tersebut. Selama penyelidikan ini, akuntan menguji sedikitnya dua buku perusahaan para. Laporannya diuraikan dalam buku Sawbridge and Company, oleh Charles Snell, Writing Master and Accountant in Foster Lane, London. Amerika Serikat berhutang konsep tujuan Akuntan Publik terdaftar pada Inggrisyang telah memiiki Chartered Accountant di abad ke 19.

Akuntansi modern

Label:


Prinsip inti akuntansi keuangan modern ada pada sistem pembukuan berpasangan. Sistem ini meliputi pembuatan paling tidak dua masukan untuk setiap transaksi: satu debitpada suatu akun, dan satu kredit terkait pada akun lain. Jumlah keseluruhan debit harus selalu sama dengan jumlah keseluruhan kredit. Cara ini akan memudahkan pemeriksaan jika terjadi kesalahan. Cara ini diketahui pertama kali digunakan pada abad pertengahan di Eropa, walaupun ada pula yang berpendapat bahwa cara ini sudah digunakan sejak zaman Yunani kuno.
Kritik mengatakan bahwa standar praktik akuntansi tidak banyak berubah sejak dulu. Reformasi akuntansi dalam berbagai bentuk selalu terjadi pada tiap generasi untuk mempertahankan relevansi pembukuan dengan aset kapital atau kapasitas produksi. Walaupun demikian, hal ini tidak mengubah prinsip-prinsip dasar akuntansi, yang memang diharapkan tidak bergantung pada pengaruh ekonomi seperti itu.
Akuntansi sebagai suatu seni yang mendasarkan pada logika matematik - sekarang dikenal sebagai “pembukuan berpasangan” (double-entry bookkeeping) - sudah dipahami di Italia sejak tahun 1495 pada saat Luca Pacioli (1445 - 1517), yang juga dikenal sebagai Friar (Romo) Luca dal Borgo, mempublikasikan bukunya tentang “pembukuan” di Venice. Buku berbahasa Inggris pertama diketahui dipublikasikan di London oleh John Gouge atau Gough pada tahun 1543.
Sebuah buku ringkas menampilkan instruksi akuntansi juga diterbitkan pada tahun 1588 oleh John Mellis dari Southwark, didalamnya memuat perkataannya, "I am but the renuer and reviver of an ancient old copie printed here in London the 14 of August 1543: collected, published, made, and set forth by one Hugh Oldcastle, Scholemaster, who, as appeareth by his treatise, then taught Arithmetics, and this booke in Saint Ollaves parish in Marko Lane." John Mellis merujuk pada fakta bahwa prinsip akuntansi yang dia jelaskan (yang merupakan sistem sederhana dari masukan ganda/double entry) adalah "after the forme of Venice".
Pada awal abad ke 18, jasa dari akuntan yang berpusat di London telah digunakan dalam suatu penyelidikan seorang direktur South Sea Company, yang tengah memperdagangkan bursa perusahaan tersebut. Selama penyelidikan ini, akuntan menguji sedikitnya dua buku perusahaan para. Laporannya diuraikan dalam buku Sawbridge and Company, oleh Charles Snell, Writing Master and Accountant in Foster Lane, London. Amerika Serikat berhutang konsep tujuan Akuntan Publik terdaftar pada Inggris yang telah memiiki Chartered Accountant di abad ke 19.

Akuntansi

Label:


Akuntansi adalah pengukuran, penjabaran, atau pemberian kepastian mengenai informasi yang akan membantu manajer, investor, otoritas pajak dan pembuat keputusan lain untuk membuat alokasi sumber daya keputusan di dalam perusahaan, organisasi, dan lembaga pemerintah. Akuntansi adalah seni dalam mengukur, berkomunikasi dan menginterpretasikan aktivitas keuangan. Secara luas, akuntansi juga dikenal sebagai "bahasa bisnis".[1] Akuntansi bertujuan untuk menyiapkan suatu laporan keuangan yang akurat agar dapat dimanfaatkan oleh para manajer, pengambil kebijakan, dan pihak berkepentingan lainnya, seperti pemegang saham, kreditur, atau pemilik. Pencatatan harian yang terlibat dalam proses ini dikenal dengan istilah pembukuan. Akuntansi keuangan adalah suatu cabang dari akuntansi dimana informasi keuangan pada suatu bisnis dicatat, diklasifikasi, diringkas, diinterpretasikan, dan dikomunikasikan. Auditing, satu disiplin ilmu yang terkait tapi tetap terpisah dari akuntansi, adalah suatu proses dimana pemeriksa independen memeriksa laporan keuangan suatu organisasi untuk memberikan suatu pendapat atau opini - yang masuk akal tapi tak dijamin sepenuhnya - mengenai kewajaran dan kesesuaiannya dengan prinsip akuntansi yang berterima umum.
Praktisi akuntansi dikenal sebagai akuntan. Akuntan bersertifikat resmi memiliki gelar tertentu yang berbeda di tiap negara. Contohnya adalah Chartered Accountant (FCA, CA or ACA), Chartered Certified Accountant (ACCA atau FCCA), Management Accountant(ACMA, FCMA atau AICWA), Certified Public Accountant (CPA), dan Certified General Accountant (CGA). Di Indonesia, akuntan publik yang bersertifikat disebut CPA Indonesia (sebelumnya: BAP atau Bersertifikat Akuntan Publik).
Akuntansi adalah pengukuran, penjabaran, atau pemberian kepastian mengenai informasi yang akan membantu manajer, investor, otoritas pajak dan pembuat keputusan lain untuk membuat alokasi sumber daya keputusan di dalam perusahaan, organisasi, dan lembaga pemerintah. Akuntansi adalah seni dalam mengukur, berkomunikasi dan menginterpretasikan aktivitas keuangan. Secara luas, akuntansi juga dikenal sebagai "bahasa bisnis".[1] Akuntansi bertujuan untuk menyiapkan suatu laporan keuangan yang akurat agar dapat dimanfaatkan oleh para manajer, pengambil kebijakan, dan pihak berkepentingan lainnya, seperti pemegang saham, kreditur, atau pemilik. Pencatatan harian yang terlibat dalam proses ini dikenal dengan istilah pembukuan. Akuntansi keuangan adalah suatu cabang dari akuntansi dimana informasi keuangan pada suatu bisnis dicatat, diklasifikasi, diringkas, diinterpretasikan, dan dikomunikasikan. Auditing, satu disiplin ilmu yang terkait tapi tetap terpisah dari akuntansi, adalah suatu proses dimana pemeriksa independen memeriksa laporan keuangan suatu organisasi untuk memberikan suatu pendapat atau opini - yang masuk akal tapi tak dijamin sepenuhnya - mengenai kewajaran dan kesesuaiannya dengan prinsip akuntansi yang berterima umum.
Praktisi akuntansi dikenal sebagai akuntan. Akuntan bersertifikat resmi memiliki gelar tertentu yang berbeda di tiap negara. Contohnya adalah Chartered Accountant (FCA, CA or ACA), Chartered Certified Accountant (ACCA atau FCCA), Management Accountant (ACMA, FCMA atau AICWA), Certified Public Accountant (CPA), dan Certified General Accountant (CGA). Di Indonesia, akuntan publik yang bersertifikat disebut CPA Indonesia (sebelumnya: BAP atau Bersertifikat Akuntan Publik).

Audit

Label: , ,

Audit atau pemeriksaan dalam arti luas bermakna evaluasi terhadap suatu organisasi, sistem, proses, atau produk. Audit dilaksanakan oleh pihak yang kompeten, objektif, dan tidak memihak, yang disebut auditor. Tujuannya adalah untuk melakukan verifikasi bahwa subjek dari audit telah diselesaikan atau berjalan sesuai dengan standar, regulasi, dan praktik yang telah disetujui dan diterima.

Audit keuangan

Audit keuangan adalah audit terhadap laporan keuangan suatu entitas (perusahaan atau organisasi) yang akan menghasilkan pendapat (opini) pihak ketiga mengenai relevansi, akurasi, dan kelengkapan laporan-laporan tersebut.
Audit keuangan umumnya dilaksanakan oleh kantor akuntan publik atau akuntan publik sebagai auditor independen dengan berpedoman pada standar profesional akuntan publik.

Audit operasional

Audit Operasional adalah pengkajian atas setiap bagian organisasi terhadap prosedur operasi standar dan metode yang diterapkan suatu organisasi dengan tujuan untuk mengevaluasi efisiensi, efektivitas, dan keekonomisan (3E).

Audit ketaatan

Audit Ketaatan adalah proses kerja yang menentukan apakah pihak yang diaudit telah mengikuti prosedur, standar, dan aturan tertentu yang ditetapkan oleh pihak yang berwenang.

Audit investigatif

Audit Investigatif adalah: 1. "Serangkaian kegiatan mengenali (recognize), mengidentifikasi (identify), dan menguji (examine) secara detail informasi dan fakta-fakta yang ada untuk mengungkap kejadian yang sebenarnya dalam rangka pembuktian untuk mendukung proses hukum atas dugaan penyimpangan yang dapat merugikan keuangan suatu entitas (perusahaan/organisasi/negara/daerah)." 2. "a search for the truth, in the interest of justice and in accordance with specification of law" (di negara common law)
Jadi, audit itu adalah suatu rangkaian kegiatan yang menyangkut:
  1. Proses pengumpulan dan evaluasi bahan bukti
  2. Informasi yang dapat diukur. Informasi yang dievaluasi adalah informasi yang dapat diukur. Hal-hal yang bersifat kualitatif harus dikelompokkan dalam kelompok yang terukur, sehingga dapat dinilai menurut ukuran yang jelas, seumpamanya Baik Sekali, Baik, Cukup, Kurang Baik, dan Tidak Baik dengan ukuran yang jelas kriterianya.
  3. Entitas ekonomi. Untuk menegaskan bahwa yang diaudit itu adalah kesatuan, baik berupa Perusahaan, Divisi, atau yang lain.
  4. Dilakukan oleh seseorang (atau sejumlah orang) yang kompeten dan independen yang disebut sebagai Auditor.
  5. Menentukan kesesuaian informasi dengan kriteria penyimpangan yang ditemukan. Penentuan itu harus berdasarkan ukuran yang jelas. Artinya, dengan kriteria apa hal tersebut dikatakan menyimpang.
  6. Melaporkan hasilnya. Laporan berisi informasi tentang kesesuaian antara informasi yang diuji dan kriterianya, atau ketidaksesuaian informasi yang diuji dengan kriterianya serta menunjukkan fakta atas ketidaksesuaian tersebut.

Arisan

Label:


Arisan adalah kelompok orang yang mengumpul uang secara teratur pada tiap-tiap periode tertentu. Setelah uang terkumpul, salah satu dari anggota kelompok akan keluar sebagai pemenang. Penentuan pemenang biasanya dilakukan dengan jalan pengundian, namun ada juga kelompok arisan yang menentukan pemenang dengan perjanjian.
Di Indonesia, dalam budaya arisan, setiap kali salah satu anggota memenangkan uang pada pengundian, pemenang tersebut memiliki kewajiban untuk menggelar pertemuan pada periode berikutnya arisan akan diadakan.
Arisan beroperasi di luar ekonomi formal sebagai sistem lain untuk menyimpan uang, namun kegiatan ini juga dimaksudkan untuk kegiatan pertemuan yang memiliki unsur "paksa" karena anggota diharuskan membayar dan datang setiap kali undian akan dilaksanakan.

Anjak piutang

Label: ,


Anjak piutang (bahasa Inggris: factoring) adalah suatu transaksi keuangan sewaktu suatu perusahaan menjual piutangnya (misalnya tagihan) dengan memberikan suatu diskon. Ada tiga perbedaan antara anjak piutang dan pinjaman bank. Pertama, penekanan anjak piutang adalah pada nilai piutang, bukan kelayakan kredit perusahaan. Kedua, anjak piutang bukanlah suatu pinjaman, melainkan pembelian suatu aset (piutang). Terakhir, pinjaman bank melibatkan dua pihak, sedangkan anjak piutang melibatkan tiga pihak.
Tiga pihak yang terlibat dalam anjak piutang adalah penjual, debitur, dan pihak yang membiayai (factor). Penjual adalah pihak yang memiliki piutang (biasanya untuk layanan yang diberikan atau barang yang dijual) dari pihak kedua, debitur. Penjual selanjutnya menjual satu atau lebih tagihannya dengan potongan atau diskon ke pihak ketiga, suatu lembaga keuangan khusus untuk mendapatkan uang dalam bentuk kas. Debitur akan membayar langsung ke perusahaan pembiayaan dengan jumlah penuh sesuai nilai tagihan.
Manfaat Anjak Piutang adalah:
  • Menurunkan biaya produksi
  • Memberikan fasilitas pembayaran di muka
  • Meningkatkan daya saing perusahaan klien
  • Meningkatkan kemampuan perusahaan klien memperoleh laba
  • Menghindari kerugian karena kredit macet
  • Mempercepat proses ekonomi

Kurva indiferensi

Label:

Kurva indiferensi dalam mikroekonomi adalah kurva yang menggambarkan hubungan antara dua bundel barang di mana konsumen mendapatkan kepuasan yang sama (indiferen) pada tiap-tiap titik kombinasi kuantitas (Q) kedua bundel tersebut.

 Teori kurva indeferensi dikembangkan oleh Francis Ysidro Edgeworth, Vilfredo Pareto, dan kawan-kawan di awal abad ke-20. Teori ini diturunkan dari teori utilitas ordinal, yang mengasumsikan bahwa setiap orang selalu dapat mengurutkan preferensinya. Dengan kata lain, seseorang selalu dapat menentukan bahwa ia lebih menyukai barang A dibanding barang B, dan lebih suka barang B dibanding barang C, lebih suka barang C daripada barang D dan seterusnya.

Peta dan ciri dari kurva indiferensi

Sebuah grafik dari kurva indiferensi untuk seorang konsumen dihubungkan dengan tingkat utilitas/kepuasan berbeda disebut dengan peta indiferensi. Titik kembalinya tingkat kepuasan yang berbeda setiap unitnya dihubungkan dengan kurva indiferensi yang berbeda satu sama lain. Sebuah kurva indiferensi menjabarkan sebuah himpunan preferensi pribadi dan bisa berbeda pada orang satu dan lainnya.
Kurva indiferensi biasanya dijelaskan menjadi :
  1. Dijabarkan hanya pada kuadran positif (+, +) diagram Cartesius dari komoditas berdasarkan kuantitas.
  2. Melengkung secara negatif. Sebagai Kuantitas yang dikonsumsi dari satu barang (x) meningkat, kepuasan total akan naik jika tidak di kompensasikan oleh sebuah penurunan dalam kuantitas yang dikonsumsi pada barang lain (y). Sama dengan kekenyangan, dimana lebih dari barang (atau keduanya) sama derajatnya di prefrensikan untuk tidak ditingkatkan, tidak diikutsertakan. (jika utilitas U=f(x, y), U, dalam dimensi ke tiga, tidak memiliki sebuah maksimum lokal untuk semua x dan y.)
  3. lengkap, seperti semua titik dalam kurva indiferen dirangking sama besar dalam hal selera dan dirangking baik lebih atau kurang di sukai dibandingkan titik lainnya yang tidak ada dalam kurva. Jadi, dengan (2), tidak ada dua kurva yang akan bersilangan (selain non-satiasi akan dilanggar).
  4. Transitif dengan hubungan ke titik dalam kurva indiferen yang berbeda. Itu terjadi, jika tiap titik dalam I2 adalah selera (yang terbatas) pada tiap titik dalam I1, dan tiap titik dalam I3 dihubungkan ke tiap titik dalam I2, tiap titik dalam I3 dihubungkan ke tiap titik dalam I1. Sebuah lengkungan negatif dan transitifitas tidak dimasukan persilangan kurva indiferen, karena garis lurus dari kedua sisi tersebut bersilangan akan memberi rangking prefrensi yang tidak satu sisi dan intransitif.
  5. (secara terbatas) convex (dijatuhkan dari bawah). Dengan (2), preferensi convex menyebabkan sebuah pemunculan dari asal kurva indiferen. Sebagai konsumen menurunkan konsumsi dari satu barang dalam unit suksesif, jumlah besar dari barang lainnya akan dibutuhkan untuk mempertahankan kepuasan tidak berubah, efek substitusi.
Ambil a, b dan c menjadi kumpulan (vektor) dari barang, seperti kombinasi (x, y) di atas, dimana kemungkinan adanya perbedaan jumlah dari tiap barang dalam kumpulan yang berbeda. Asumsi pertama adalah kebutuhan untuk sebuah representasi yang dibuat dnegan baik dari selera stabil untuk para konsumen sebagai agen ekonomi, asumsi kedua disesuaikan.
Rasionalitas (dalam hubungannya dalam konteks matematik yang umum): Keterselesaian + transtifitas. Untuk rangking pemberian prefrensi, konsumen bisa memilih kumpulan yang terbaik antara a, b dan c dari terbawah ke tertinggi.
Kontinuitas: Ini berarti kamu bisa memilih untuk mengonsumsi berapapun jumlah barang. Contohnya, saya bisa minum 11 mL soda, atau 12mL, atau 132 mL. Saya tidak dipaksa untuk meminum dua liter atau tidak sama sekali. Lihat juga fungsi kontinuitas dalam matematik.
Dari ciri yang tersisa di atas, seharusnya, ciri (5) (kofeksitas) telah dilanggar oleh munculnya kurva indiferen keluar dari asal konsumen tertentu dengan memberikan dorongan ke anggaran. Teori konsumen kemudian menyebabkan konsumsi kosong untuk satu dari dua barang, katakanlah barang Y, dalam ekuilibirium ke anggaran konsumen. Ini akan mencontohkan sebuah solusi pojok. Lebih jauh, penurunan dalam harga barang Y di atas jarak tertentu mungkin akan meninggalkan jumlah/kuantitas yang diminta tidak akan berubah dari kosong (0) dan sesudahnya dimana penurunan harga selanjutnya mengganti semua pendapatan dan konsumsi jauh-jauh dari X dan Y. Rasio dari implikasi tersebut mensugestikan kenapa konfeksitas biasanya diasumsikan juga.

Contoh dari Kurva Indiferensi

Dalam Gambar 1, konsumen akan lebih ke I3 daripada ke I2, dan akan lebih ke I2 daripada I1, tetapi tidak peduli dimana sang konsumen berada dalam kurva indiferen yang diwakilkan. Lekukan dari sebuah kurva indiferen (dalam nilai mutlak), dikenal oleh para ekonom sebagai rasio marjinal dari subtitusi, menunjukkan rasio dimana konsumen ingin memberi satu barang untuk ditukar lebih dengan barang yang lain. Untuk kebanyakan barang rata-rata marjinal dari subtitusi tidak tetap sehingga kurva indiferen mereka melekuk dengan tajam. Kurva tersebut merupakan konfeks dari aslinya, menjelaskan efek negatif subtitusi. Selaras dengan kenaikan harga untuk pendapatan tetap, konsumen mencari barang subtitusi yang lebih murah pada kurva indifeen yang lebih rendah. Efek subtitusi diperkuat dengan efek pendapatan atau pendapatan nyata yang lebih rendah (Beattie-LaFrance). Sebuah contoh dari sebuah fungsi utilitas yang membuat kurva indiferen dari jenis ini adalah fungsi Coubb-Douglas

U\left(x,y\right)=x^\alpha y^{1-\alpha}, 0 \leq \alpha \leq 1.

Jika barang merupakan subtitusi sempurna maka kurva indiferen akan menjadi garis yang paralel karena konsumen akan meninginkan pertukaran pada sebuah rasio tetap. Rata-rata marjinal dari subtitusi selalu konstan. Contohnya yang diambil dari fungsi utilitas dihubungkan dengan kurva indiferen seperti ini akan menjadi

U\left(x,y\right)=\alpha x + \beta y.

Jika barang merupakan komplementer sempurna maka kurva indiferensi akan menjadi berbentuk L. Contohnya seperti jika kamu mempunyai sebuah resep kue yang terdiri dari 3 cangkir tepung dan 1 cangkir gula. Tidak peduli berapapun tepung ekstra yang dipunya, tidak akan bisa membuat kue lebih banyak lagi karena tidak adanya kelebihan gula. Contoh lain dari komplementer sempurna adalah sepatu kiri dan sepatu kanan. Konsumen tidak menjadi lebih untung jika mempunyai banyak sepatu kanan jika hanya mempunyai sepatu kiri satu buah. Sepatu kanan tambahan memiliki utilitas marjinal kosong (0) tanpa adanya sepatu kiri yang sejumlah. Rata-rata marjinal dari subtitusi bisa kosong atau tak terbatas. Contoh dari tipe fungsi utilitas yang memiliki peta indiferensi seperti yang di atas adalah .

U\left(x,y\right)= \min \{ \alpha x, \beta y \}.
Bentuk berbeda dari kurva menyebabkan respon yang berbeda kepada perubahan harga seperti yang ditunjukkan oleh analisa permintaan dalam teori konsumen. Hasilnya akan diterangkan disini. Sebuah garis harga dan anggaran ynang berubah yang membuat seorang konsumen dalam ekuilibrium dalam kurva indiferensi yang sama:
Dalam Gambar 1 akan mengurangi jumlah yang diminta dari sebuah barang dengan halus sebagai harga yang naik secara relatif untuk barang tersebut.
Dalam Gambar 2 akan tidak memberi efek dalam permintaan kuantitas dari kedua barang atau mengubah kuantitas yang diminta dari satu anggaran ke yang lain.
Dalam Gambar 3 tidak akan memberi efek pada ekuilibrium permintaan jumlah, karena garis anggaran akan berputar disekitar sudut dari kurva indiferensi.

Relasi Prefrensi dan Utilitas

Teori pilihan resminya mewakilkan konsumen dengan sebuah relasi prefrensi, dan menggunakan penggambaran ini untuk mendapatkan kurva indiferensi.
Ide tentang sebuah kurva indiferensi merupakan penggambaran jelas: Jika seorang konsumen mendapatkan kepuasan yang sama dengan 1 apel dan 4 pisang, 2 apel dan 2 pisang, atau 5 apel dan 1 pisang, kombinasi ini akan berada dalam kurva indiferensi yang sama.

Relasi Prefrensi

Masukkan
A\; = sebuah set dari alternatif yang eksklusif secara mutual di antara lainnya dimana konsumen bisa memilih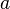
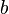a\; dan b\; = elemen umum dari A\;.
Dalam bahasa dari contoh di atas, syarat A\; dibuat dari kombinasi dari apel dan pisang. Simbol a\; merupakan kombinasi, seperti 1 apel dan 4 pisang dan b\; merupakan kombinasi lain seperti 2 apel dan 2 pisang.
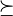Sebuah relasi prefrensi, denotasi \succeq, adalah sebuah relasi biner didefinisi dalam set A\;.
Pernyataan
a\succeq b\;
Dijelaskan sebagai 'a\; diprefrensikan tidak terlalu kuat ke b\;. Maka, a\; setidaknya sama baik dengan b\; (dalam kepuasan prefrensi)
Pernyataan
a\sim b\;
Dijelaskan sebagai'a\; direferensikan ke b\;, dan b\; direfrensikan secara lemah ke a\;. Maka, satu merupakan indiferen ke pilihan dari a\; atau b\;, tidak berarti mereka tidak diinginkan tetapi mereka sama baik dalam prefrensi kepuasan.
Pernyataan
a\succ b\;
Dijelaskan sebagai 'a\; diprefrensikan secara lemah ke b\;, tetapi b\; tidak diprefrensikan secara lemah ke a\;. Dikatakan bahwa a\; diprefrensikan secara terbatas ke b\;.
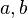Relasi prefrensi \succeq adalah komplit jika semua pasangan a,b\; bisa diberi peringkat. Relasitersebut merupakan relasi transitif jika kapanpun a\succeq b\; dan b\succeq c,\; lalu a\succeq c\;.
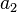masukan sebuah elemen tertentu dari pasangan A\;, seperti a_0\;. Seharusnya salah satu membangun daftar dari elemen lain dari A\; yang merupakan indiferen, di mata konsumen, ke a_0\;. Denotasikan elemen pertama dalam daftar ini dengan a_1\;, yang kedua dengan a_2\; dan seterusnya. Set \{a_i:i\geq 0\} membentuk sebuah kurva indiferensi karena a_i\sim a_j\; untuk semua i,j\geq 0\;.

Hubungan Formal ke Teori Utilitas

Dalam contoh di atas, sebuah elemen a\; dari set A\; dibuat dari dua angka: angka dari apel, sebut saja x,\; dan angka dari pisang, sebut y.\;
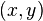Dalam teori utilitas, fungsi utilitas dari agen adalah fungsi yang memberi peringkat semua pasangan dari bundel konsumsi dengan urutan prefrensi (kelengkapan) maka adanya set tiga atau lebih bundel membentuk sebuah relasi transitif. Ini berarti untuk setiap bundel \left(x,y\right) ada sebuah relasi unik, U\left(x,y\right), menujukkan utilitas (kepuasan) relasinya yang diasosiasikan dengan \left(x,y\right).
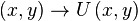Relasi \left(x,y\right)\to U\left(x,y\right) disebut dengan fungsi utilitas. Jarak dari fungsi tersebut merupakan sebuah set dari bilangan real. Nilai sebenarnya dari fungsi tersebut tidak penting. Hanya peringkat dari nilai-nilai tersebut memiliki isi untuk teori tersebut. Lebih tepatnya, jika U(x,y)\geq U(x',y') lalu bundel \left(x,y\right) dijelaskan sebagai setidaknya sama baik dengan bundel \left(x',y'\right). Jika U\left(x,y\right)>U\left(x',y'\right), bundel \left(x,y\right) dijelaskan secara terbatas diprefrensikan ke bundel \left(x',y'\right).
Masukan sebuah bundel tertentu \left(x_0,y_0\right) dan ambil derifatif total dari U\left(x,y\right) mengenai titik ini:
dU\left(x_0,y_0\right)=U_1\left(x_0,y_0\right)dx+U_2\left(x_0,y_0\right)dy  atau, tanpa kehilangan generalitas,
\frac{dU\left(x_0,y_0\right)}{dx}= U_1(x_0,y_0).1+ U_2(x_0,y_0)\frac{dy}{dx} (Eq. 1)
Dimana U_1\left(x,y\right) merupakan derifatif parsial dari U\left(x,y\right) dengan mengurut ke argumen pertama, dievaluasikan pada \left(x,y\right). (Seperti untuk U_2\left(x,y\right). )
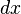Kurva indiferensi melalui \left(x_0,y_0\right) harus mengirim pada tiap bundel dalam kurva dalam tingkat utilitas yang sama dengan bundel \left(x_0,y_0\right). Dengan kata lain, jika salah satu akan mengganti jumlah x\, dengan dx\,, satu tersebut harus mengubah kuantitas dari y\, dengan jumlah dy\, seperti itu, akhirnya, tidak ada perubahan pada U:
\frac{dU\left(x_0,y_0\right)}{dx}= 0, atau, mengganti 0 menjadi (Eq. 1) di atas untuk memecahkan dy/dx:
\frac{dU\left(x_0,y_0\right)}{dx} = 0\Leftrightarrow\frac{dy}{dx}=-\frac{U_1(x_0,y_0)}{U_2(x_0,y_0)}.
Maka, rasio dari utilitas marjinal memberi nilai absolut dari lekukan kurva indiferens pada titik \left(x_0,y_0\right). Rasio ini disebut dengan rasio marjinal dari subtitusi antara x\, dan y\,.

Utilitas Linier

Jika fungsi utilitas merupakan bentuk dari U\left(x,y\right)=\alpha x+\beta y maka utilitas marjinal dari x\, adalah U_1\left(x,y\right)=\alpha dan utilitas marjinal dari y\, adalah U_2\left(x,y\right)=\beta. Lekukan dari kurva indiferens adalah, selanjutnya,
\frac{dx}{dy}=-\frac{\beta}{\alpha}.
Melihat dimana lekukan tersebut tidak bergantung pada x\, atau y\,: Kurva indiferens merupakan garis lurus.

Utilitas Cobb-Douglas

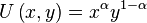Jika fungsi utilitas merupakan bentuk dari U\left(x,y\right)=x^\alpha y^{1-\alpha} utilitas marjinal dari x\, adalah U_1\left(x,y\right)=\alpha \left(x/y\right)^{\alpha-1} dan utilitas marjinal dari y\, adalah U_2\left(x,y\right)=(1-\alpha) \left(x/y\right)^{\alpha}. Rasio marjinal dari subtitusi, dan kemudian lekukannya dari kurva indiferens ialah
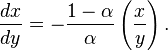
\frac{dx}{dy}=-\frac{1-\alpha}{\alpha}\left(\frac{x}{y}\right).

Utilitas CES

Sebuah CES (Constant Elasticity of Subtitusion) dalam bentuk umum ialah
U(x,y)=\left(\alpha x^\rho +(1-\alpha)y^\rho\right)^{1/\rho}
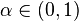dimana \alpha\in(0,1) dan \rho\leq 1. ([Cobb-Douglas]] merupakan kasus spesial dari utilitas CES, dengan \rho=0\,.) Utilitas marjinal diberi oleh
U_1(x,y)=\alpha \left(\alpha x^\rho +(1-\alpha)y^\rho\right)^{\left(1/\rho\right)-1} x^{\rho-1}
dan
U_2(x,y)=(1-\alpha)\left(\alpha x^\rho +(1-\alpha)y^\rho\right)^{\left(1/\rho\right)-1} y^{\rho-1}.
Lalu, bersama kuva indiferens,
\frac{dx}{dy}=-\frac{1-\alpha}{\alpha}\left(\frac{x}{y}\right)^{1-\rho}.
Contoh ini mungkin berguna sebagai model ekonomi dalam konteks inidivual atau permintaan agregat.

Utilitas Non Linear

Misal model Utilits sebagai berikut :
U=AXi^bi
dimana i = 1, 2, ... n Xi=Jenis barang ke i yang ingin dibeli konsumen bi=koefisien regresi A=Anggaran yang dimiliki konsumen maka banyaknya Xi optimal yang dapat dibeli konsumen adalah :
Xi=(Abi)/(Pxi.Σbi)
dimana Pxi=harga barang ke i yang dibeli konsumen Σbi = b1 + b2 + .... + bn syarat tidak ada nilai bi yang negatif

Sumber : 
  • Bruce R. Beattie and Jeffrey T. LaFrance, “The Law of Demand versus Diminishing Marginal Utility” (2006). Review of Agricultural Economics. 28 (2), pp. 263-271.
  • Volker Böhm and Hans Haller (1987). "demand theory," The New Palgrave: A Dictionary of Economics, v. 1, pp. 785-92.
  • John Geanakoplis (1987). "Arrow-Debreu model of general equilibrium," The New Palgrave: A Dictionary of Economics, v. 1, pp. 116-24.



Langganan: Postingan (Atom)

Copyright 2008 Splashpress Media | Converted by Free XML Templates | Blogging Pro Blogger | Designed by Design Disease